7.11.1.1. 数据结构之树

7.11.1.1.1. 树的概念

树是数据结构中的一种，其属于非线性数据结构的一种。树由结点和边组成，且不存在任何环的一种数据结构。

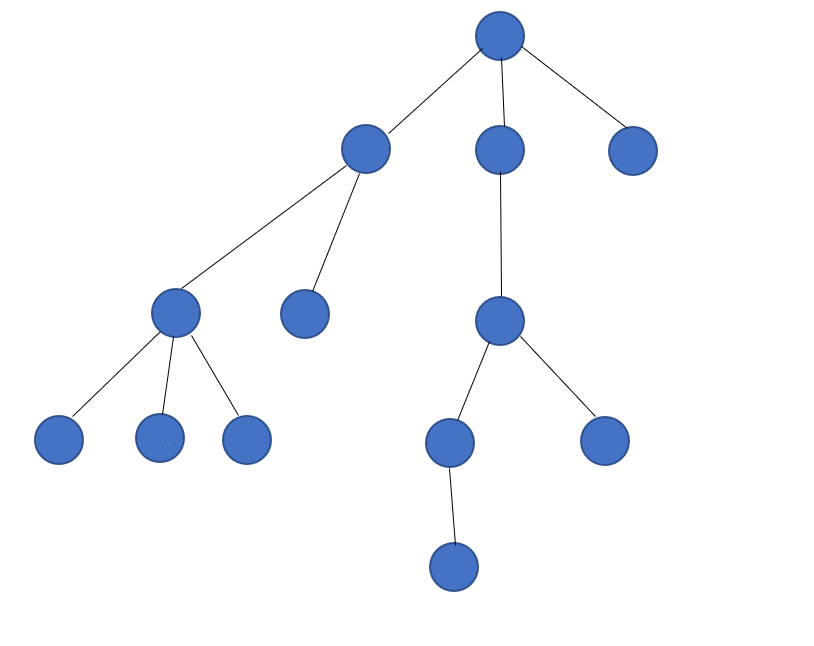
../../../_images/tree.png

  • 树的基本术语

术语

描述

节点的度

树中某个节点的子树的个数

树的度

树中各节点的度的最大值

分支节点

度不为0的节点

叶子节点

度为0的节点

孩子节点

某节点的后继节点

父节点

该节点为其孩子的父节点

兄弟节点

同一父节点的孩子节点互为兄弟节点

子孙节点

某节点所有子树中的节点

祖先节点

节点的层次

根节点为第一层(以此类推)

树的高度

树中节点的最大层次

有序树

树中节点子树按次序从左向右排列，次序不能改变

无序树

与有序树相反

  • 树的性值

  1. 树中节点数为节点度树加1(加根节点)

  2. 度为m的树中第i层最多有m^(i-1)个节点

  3. 高度为h的m次树至多有(m^h-1)/(m-1)个节点

  4. 具有n个节点的m次树的最小高度为logm(n(m-1)+1)向上取整

7.11.1.1.2. 二叉树

二叉树是n个节点的有限集合，该集合可以为空集(称为空二叉树)，或者由一个根节点和两棵互不相交的子树组成，分别称为根节点左子树和右子树

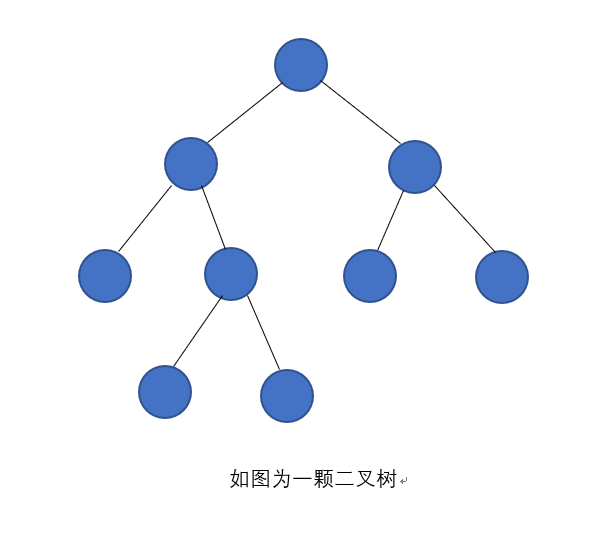
../../../_images/binary_tree.png

每一个节点中最多拥有一个左结点和右结点，并没有多余的结点，这是很明星的二叉树特征

  • 二叉树特点

  1. 每个结点最多有两颗子树，所以二叉树中不存在度大于2的结点

  2. 左子树和右子树是有顺序的，次序不能任意颠倒

  3. 即使树中某结点只有一颗子树，也要区分它是左子树还是右子树

  • 二叉树的性质

  1. 二叉树第i层上的结点数最多为2^(i-1)个结点

  2. 深度为k的二叉树最多有2^k-1个结点

  3. 包含n个结点的二叉树高度至少为log2(n+1)

  4. 在任意一颗二叉树中，若终端结点的个树为N0，度为2的结点为n2,则n0=n2+1

  • 几种特殊的二叉树

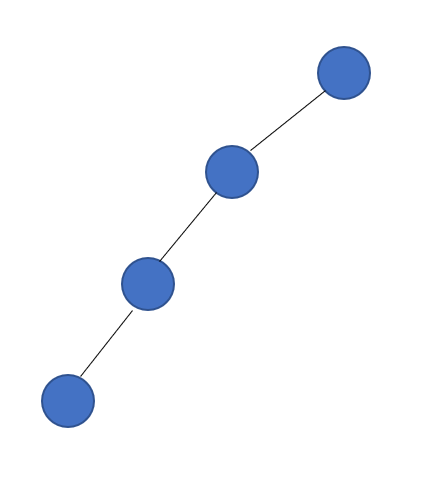
斜树: 所有结点都只有左子树的二叉树叫左写树。相反的为右斜树

../../../_images/incline_tree.png

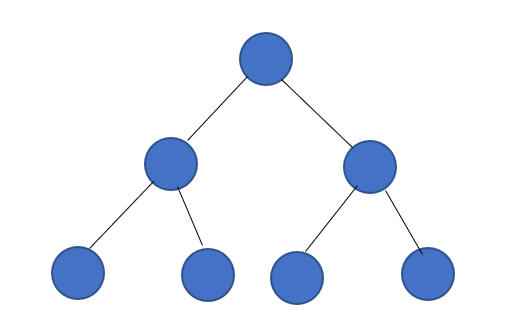
满二叉树: 在二叉树中所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的二叉树称为满二叉树

满二叉树的特点有:

  1. 叶子结点只能出现在最下一层

  2. 非叶子结点的度一定是2

  3. 在同样深度的二叉树中，满二叉树的结点个树最多，叶子数最多

../../../_images/full_tree.png

完全二叉树: 对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中的编号为i的结点在二叉树中的位置完全相同，则这颗二叉树称为完全二叉树

../../../_images/complete_tree.png

7.11.1.1.3. 二叉树的存储

二叉树的存储可以有两种方式:顺序存储和链式存储

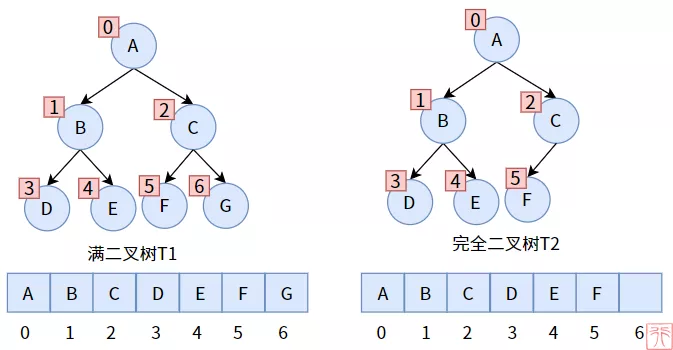
顺序存储

满二叉树

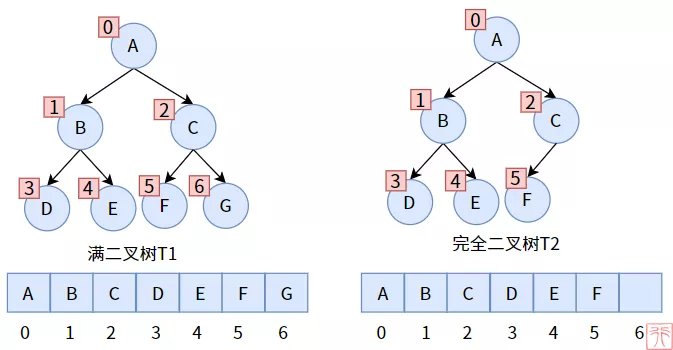
../../../_images/full_tree_save.png

完全二叉树

../../../_images/complete_tree_save.png

非满、完全二叉树

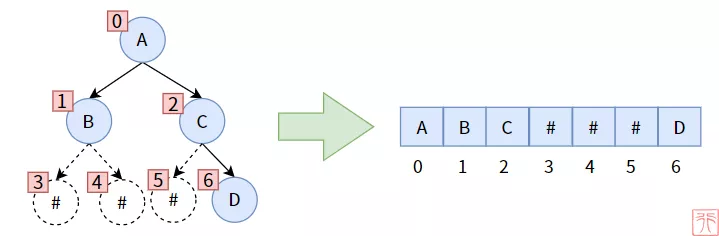
../../../_images/tree_save.png

这种存储的缺点是，数组中可能会有大量空间未使用，造成浪费

链式存储

链式存储则采用链表的方式进行数据存储。也是较为常见的存储方式

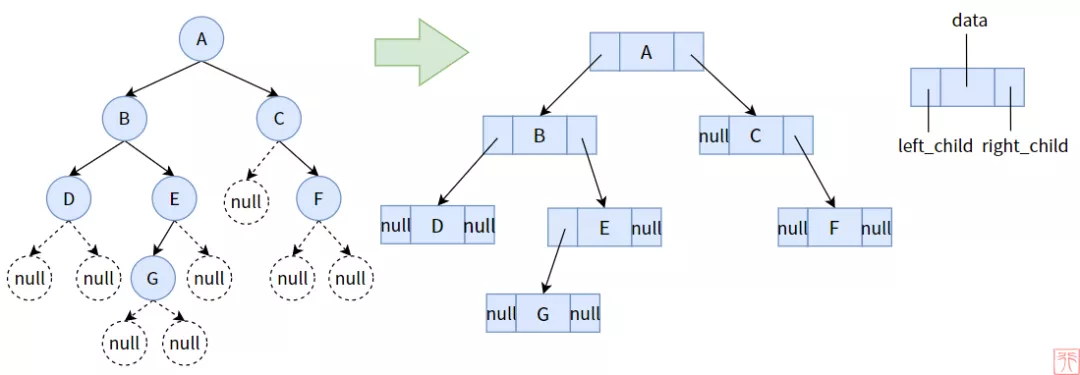
../../../_images/tree_link_save.png

一颗二叉树的结点设计一定要有如下内容：

  1. 结点元素，data域，用来存储数据可以是int，char等基本类型，也可以是struct等复合数据类型

  2. 左孩子结点，left指针

  3. 右孩子结点，right指针

  4. 父结点(可选)，parent指针

struct node
{
    int data;
    struct node* left;
    struct node* right;
};

struct Tree
{
    struct node* root;
};

7.11.1.1.3.1. 树的创建

void insert(struct tree* t, int value)
{
    struct node* node = (struct node*)malloc(sizeof(struct node));
    node->data = value;
    node->left = NULL;
    node->right = NULL;

    if(t->root == NULL)
    {
        t->root = node;
    }
    else
    {
        struct node* tmp = t->root;
        while(tmp != NULL)
        {

        }
    }
}

7.11.1.1.4. 二叉树的遍历

二叉树的遍历可以总结为以下三句话

  1. 先序遍历: 根左右

  2. 中序遍历: 左根右

  3. 后序遍历: 左右根

7.11.1.1.4.1. 先序遍历

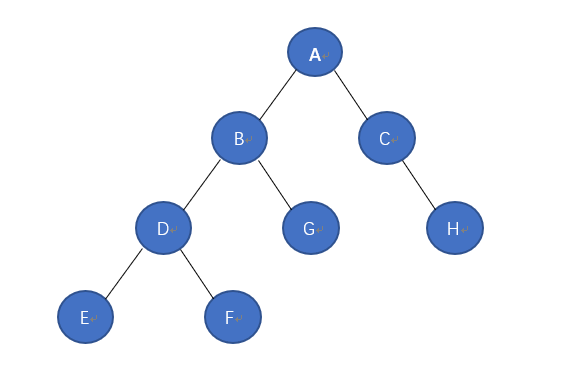
../../../_images/pre_traversal.png

这个二叉树的先序遍历访问顺序就是: ABDEFGCH

/* Pre-Traverse Binary-Tree */
static void Preorder_Traverse_BinaryTree(struct binary_node *node)
{
    if (node == NULL) {
        return;
    } else {
        printf("%d ", node->idx);
        /* Traverse left child */
        Preorder_Traverse_BinaryTree(node->left);
        /* Traverse right child */
        Preorder_Traverse_BinaryTree(node->right);
    }
}

7.11.1.1.4.2. 中序遍历

../../../_images/pre_traversal.png

这个二叉树的中序遍历访问顺序就是：EDFBGACH

/* Midd-Traverse Binary-Tree */
static void Middorder_Traverse_BinaryTree(struct binary_node *node)
{
    if (node == NULL) {
        return;
    } else {
        Middorder_Traverse_BinaryTree(node->left);
        printf("%d ", node->idx);
        Middorder_Traverse_BinaryTree(node->right);
    }
}

7.11.1.1.4.3. 后序遍历

../../../_images/pre_traversal.png

这个二叉树的后续遍历访问顺序就是: EFDGBHCA

/* Post-Traverse Binary-Tree */
static void Postorder_Traverse_BinaryTree(struct binary_node *node)
{
    if (node == NULL) {
        return;
    } else {
        Postorder_Traverse_BinaryTree(node->left);
        Postorder_Traverse_BinaryTree(node->right);
        printf("%d ", node->idx);
    }
}